This article is about an algorithmic problem. I did not find a solution to this problem either thinking about it, searching the net or talking to friends. The problem itself is simple. At the first reading, it may lure the reader into a false sense of simplicity. You may feel that this should not be an issue. But it is. At least for me.

Nothing Java. Nothing programming other than it is about an algorithmic problem.

1. Problem Statement

There is an array of \(2n\) elements. The array is \(A=\{a_1,a_2, ... , a_n, b_1, b_2, ... , b_b\}\). What steps should be taken to rearrange the array so that \(A=\{a_1,b_1,a_2,b_2, ... , a_n,b_n\}\) with limited, maximum \(O(1)\) memory, and \(O(n)\) time.

2. ChatGPT solution

Sine generative AI is sweeping the media and the internet; I thought that I should try to use it to solve the problem. After all, if it takes my job just in a few years, at least we can let it do some work for us till then.

Here is the answer, no surprise: totally wrong:

Warning
Wrong answer from ChapGPT

To rearrange the array \(A=\{a_1,a_2, ... , a_n, b_1, b_2, ... , b_n\}\) into \(A=\{a_1,b_1,a_2,b_2, ... , a_n,b_n\}\) with limited, maximum O(1) memory, and \(O(n)\) time you can follow the steps below:

Traverse the array and for each element at index \(i\), swap it with the element at index \(i+n\).

For i=1 to n:
  Swap A[i] with A[i+n]

After the traversal is complete, the array will be rearranged as \(A=\{a_1,b_1,a_2,b_2, ... , a_n,b_n\}\). The above algorithm has a time complexity of O(n) and uses only O(1) memory as only a constant number of variables are used for swapping elements in the array.

After following these steps, the original array \(A=\{a_1,a_2, ... , a_n, b_1, b_2, ... , b_n\}\) would be rearranged as \(A=\{a_1,b_1,a_2,b_2, ... , a_n,b_n\}\).

The described algorithm is \(O(n)\) time and \(O(1)\) memory, but the resulting array will be \(A=\{b_1,b_2, ... , b_n,a_1,a_2, ... , a_n\}\).

Note
 I am not worried about being replaced by an AI as a software engineer. Yet.

3. Without the \( O(1)\)memory constraint

The problem is not that hard if you do not have the \(O(1)\) memory constraint. As a matter of fact it is so easy that it can be solved even by ChapGPT. Or can it?

Note
Simpler problem, still not good answer from ChapGPT

To rearrange the array \(A={a_1,a_2, ... , a_n, b_1, b_2, ... , b_n}\) into \(A={a_1,b_1,a_2,b_2, ... , a_n,b_n}\), you can follow the steps below:

Create two new arrays, one for the \(a\) values and another for the \(b\) values. Initialize an empty array for the \(a\) values, say \(a_{new}\). Initialize an empty array for the \(b\) values, say \(b_{new}\). Traverse the original array and separate the \(a\) and \(b\) values into two separate arrays.

For i=1 to n:
Add \(a_i\) to \(a_{new}\)
Add \(b_i\) to \(b_{new}\)

For i=n+1 to 2n:
Add \(b_i\) to \(a_{new}\)
Add \(a_i\) to \(b_{new}\)

Concatenate the two new arrays in the desired order to get the final result. Concatenate \(a_{new}\) and \(b_{new}\) in the order \(a_{new}, b_{new}\) to get the desired result. After following these steps, the original array \(A={a_1,a_2, ... , a_n, b_1, b_2, ... , b_n}\) would be rearranged as \(A={a_1,b_1,a_2,b_2, ... , a_n,b_n}\).

I believe there is no need to explain why the solution is wrong, and overly complicated. The allocation of the two arrays is unnecessary. We need only one extra array of length \(2n\), say \(T\). Then the code will look:

For i=1 to n:
Add \(a_i\) to \(T\)
Add \(b_i\) to \(T\)

Voilà, you have the result in \(T\).

Note
 Still not worried.

4. Without the \( O(n)\) time constraint: \(O(n^2)\)

How about giving some extra time instead of extra memory? Let’s keep the \(O(1)\) memory constraint, but allow \(O(n^2)\) time.

This problem is also simple to solve, but for some reason, ChatGPT gave such a foolish answer that I decided not to copy here. I know, you are curious, but it has no value, totally gibberish. The solution is

  1. to take \(b_i\)out from the array for every \(i=1,n\)one by one,

  2. push every element one position higher below \(b_i\) until we get to the place where \(b_i\) will get

  3. put \(b_i\) to its place.

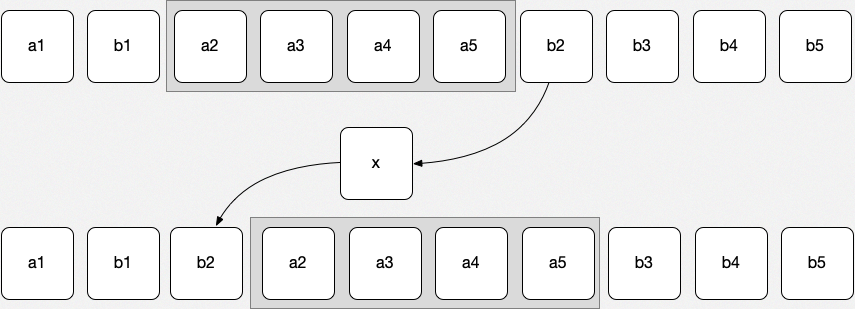
insert rearrange

For i=1 to n:
Store \(b_i\) being at the position \( n+i\)to a variable named \(x\)
Move all objects from \( 2i\) till \(n+i\) to the next position
Put \(b_i\)from the variable \(x\)to the position 2i

During the first step, we have to move \(n-1\) objects. During the second step, we have to move \(n-2\) objects, and so on. Moving all the \(b_i; i=1,n\)elements will need \( \sum_{i=1}^{n-1} (n-i) = \frac{n(n-1)}{2}\) moves. It means that this algorithm is \(O(n^2)\) time.

5. Without the \( O(n)\) time constraint: \(O(n \log n)\)

We know that there is a faster, more complex solution that is \(O(n \log n)\) time. Let’s have a look at that:

If the array length is 2, in other words, the array is \(A=\{a_1,b_1\}\), then the solution is trivial. In that case do not need to do anything, just return the array as it is.

Funny (wrong) suggestion from CoPilot

If the array is longer, then we can split it into two parts, rearrange them separately, and then merge the results.

The above sentence is not part of the normal flow of this article. I write this article with CoPilot switched on. The above sentence was suggested by CoPilot for this location.

It is fun to write articles with CoPilot switched on (pronounce it as Copy-a-Lot). I do not say it is easier, or less work. Sometimes it feels like a little kid running around and making a mess while you try to clean your flat. Rather the contrary, but undeniably more fun. Cursive words in the above paragraphs all were suggested by CoPilot.

And now, just let’s go on with the normal text of the article.

Assume that the array length is \(n=2^m\). Divide the array into four parts:

  • \(Q_1=[a_1-a_\frac n2\)],

  • \(Q_2=[a_{\frac n2+1},a_n\)],

  • \(Q_3=[b_1-b_\frac n2\)],

  • \(Q_4=[b_{\frac n2+1},b_n\)],

Swap the elements of \(Q_2\) and \(Q_3\)in a single loop:

For i=1 to \( \frac n2\):
Swap \(a_{\frac n2+i}\) and \(b_i\)

Essentially, we transform the array \(Q_1|Q_2|Q_3|Q_4\) into \(Q_1|Q_3|Q_2|Q_4\). After this, the algorithm can be applied for the sub arrays \(Q_1|Q_3\) and \(Q_1|Q_4\).

The assumption that \(n=2^m\) helps to halve the array down to length 2. When the length of the array is not some power of two, the halving is not trivial.

The algorithm running time \(T(n) = 2T(\frac n2) + O(n)\). The \(O(n)\)term is the time needed to swap the elements of \(Q_2\)and \(Q_3\). The resulting time complexity is \(O(n \log n)\).

6. Conclusion, and Takeaway

I shared this "simple" algorithmic problem with you. It is haunting me for a few years. The beauty of this problem is that it is simple, but not trivial. If you happen to know the answer, tell me! I am old enough accepting my limits, and it will more amaze me to see the solution than angry about wy I have not seen it before.

CoPilot’s suggestion

The takeaway is that you should not be afraid of simple problems.

How about AI? What is the merit of all this? Should we be afraid of AI?

The answer is no. There is no point of being afraid, generally. We can be prepared, aware, but not afraid. AI in its current form can help us solve problems, but it is immature. I expect the change and maturing of AI will be extremely rapid to a point.

It will transform how we work, but will not work instead of us or replace us. Some people will lose jobs, but new jobs will be created.

In the 1950s, people were afraid of computers. As a matter of fact, the women doing the numerical calculations were called computers. Their job does not exist today, but it did not disappear from day one to the next. It took years to disappear. We still do some calculations by hand. We still use calculators on the job site. There is even an anachronistic calculator app on the iPhone.

Something similar will happen with AI. The change will be gradual. We will have time to adapt. AI development is fast, and we feel that the development of new technologies speeds up. However, this speed is limited by the adoption rate of humans. Humans do not change that fast.

Comments

Please leave your comments using Disqus, or just press one of the happy faces. If for any reason you do not want to leave a comment here, you can still create a Github ticket.